Forward Curve

A forward curve displays the discount rates neeed to convert from a Present Value to its Future Value.
Also known as Forecast Curves, Hedge Curves, Accreting Curves or Forward-Forward Curves.

A forward curve is the interest rate for borrowing over a future time period
A forward rate refers to a period, not a specific date
A forward curve always refers to a period.
For example the 3M forward curve shows the following points:

from today - starting today, lasting for 3 months
1M - starting in 1 month, lasting for 3 months
6M - starting in 6 months, lasting for 3 months
1Y - starting in 1 year, lasting for 3 months

It shows the market expected interest rate for a period in the future.

This is the cost of borrowing when you are making payments in the future.

A forward rate is the discount rate used to calculate the value of something in the future.
A forward rate is the implied interest rate that would be used for an investment in the future.
Implies the interest rate that would be used on a date in the future

rate between two future dates

Theoretical Curve

These are "implied" forward rates.
The forward yield is the interest rate implied by a zero coupon rate.
Forward rates are a type of market view on where interest rates will be (or should be) in the future
Forward rates are the markets expectation of future rates.
Forward rates are not a prediction of future rates.

The forward yield curve is a plot of forward rates against maturity.
The forward yield curve is the interest rate implied by the zero coupon rates for period of time in the future.

These are used to work out the cash flows in an interest rate swap

Assumptions

1) Markets should be arbitrage free (ie you cant make money unless there is a risk involved)
2) A 1 year investment in treasury bills should produce the same return as 2 consecutive 6-month investments in treasury bills.
The 6-month rate you would get four 6-months periods from now is know as the 2 year forward rate denoted:

Relationship between Spot and Forward

There is a mathematical equivalence between spot rates and forward rates.
We can see that the spot yield is the geometric mean of the forward rates.

Calculate from Par Curve

Also called Full Coupon Yield Curve, par yield curve, par curve,

When a bond is priced at par, the yield to maturity is equal to the coupon rate.
This type of curve is only used in the primary market when new bonds are being issued.
Only really used in the primary market to set the coupons for new issues.
This curve is a graph of theoretical securities with prices at par.

The par yield is the coupon rate that causes the bond price to equal its face value.
The par yield is equal to the coupon rate for bonds priced at par.
On the run treasury bonds trade very close to par.

If the spot curve is upward slowing the par curve is below the spot curve
If the spot curve is downward slowing the par curve is above the spot curve

Creating

A par curve is a constructed curve where each point represents the yield on a coupon paying treasury priced at par.
This yield curve is constructed by plotting the yield to maturity against the term to maturity for bonds trading at (or near) par.
This curve can be derived directly from bonds in the market that are trading at (or near) par
If bonds are not trading at (or near) par then the yield curve will be distorted

This gives a better indication/measure of where current rates are at a particular maturity.
The par yield curve plots yield to maturity against terms to maturity for current bonds trading at par.

Creating - Using the Zero Coupon Curve

When bonds are not trading at (or near) par this curve can be derived by iteration using the spot yield curve.
When bonds are trading away from par, the par yield curve will be distorted.

Coupon Calculation for New Issues

For those involved in the primary market this type of yield curve is used to determine the required coupon when a new bond is issued at par.
Consider that par yields on 1 year, 2 year and 3 year bonds are 5%, 5.25% and 5.75% respectively.
This implies that a new 2 year bond would require a coupon of 5.25% if it was ussued at par.

Example

The par yield is the coupon rate that causes the bond price to equal its face value.
Lets assume we have the following treasury zero rates:
6 months - 5%
12 months - 5.8%
18 months - 6.4%
24 months - 6.8%
What is the par yield of a 2 year bond with principal of $100 that pays a semi-annual coupon
Lets assume that "c" is the coupon paid annually (ie the par yield)

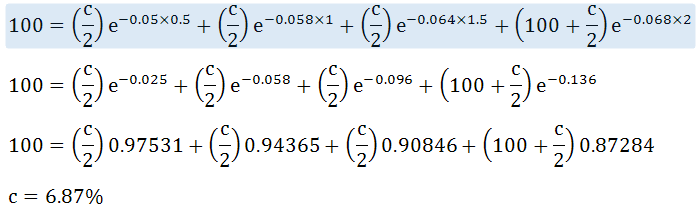The par yield is 6.87% per annum with semi-annual coupounding

This can be calculated using the Goal Seek functionality

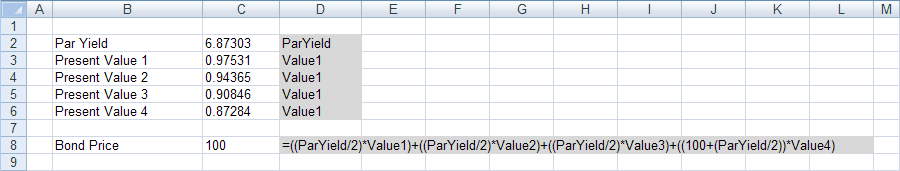Calculate from Spot Curve

You can derive the forward rate from a spot rate using this equation

If the spot curve is upward sloping the forward curve is above the spot curve
If the spot curve is downward sloping the forward curve is below the spot curve

Calculate from Spot Rates

Supposing that a bank assesses and quotes the following rates to a company, based on the annual spot yield curve for that company's risk class:

One-year: 3.50%
Two-year: 4.60%
Three-year: 5.40%
Four-year: 6.10%
Five-year: 6.30%

This indicates that the company would have to: pay interest at 3.50% if it wants to borrow a sum of money for one year; pay interest at 4.60% per year if it wants to borrow a sum of money for two years; pay interest at 5.40% per year if it wants borrow a sum of money for three years; and so on.

Alternatively, for a two-year loan, the company could opt to borrow a sum of money for only one year, at an interest rate of 3.50%, and then again for another year, commencing in one year's time, instead of borrowing the money for a total of two years.

Although the company would be uncertain about the interest rate in one year's time, it could request a forward rate from the bank that is fixed today - for example, through a 12v24 forward rate agreement (FRA). The question then arises: how may the value of the 12v24 FRA be determined?

A forward rate commencing in one year for a borrowed sum lasting a year can be calculated as follows:

In summary:

Supposing the company wants to borrow a sum of money for three years on the basis of the above rates:
i. it could pay annual interest at a rate of 5.40% in each of the three years, or
ii. it could pay interest at a rate 3.50% in the first year, 5.71% in the second year and 7.02% in the third year, or
iii. it could pay annual interest at a rate of 4.60% in each of the first two years and 7.02% in the third year.