Probability

The definition of probability is that the probability of an event is the proportion of times the event happens out of a large number of trials.
Where an event is an occurrence.
Uncertainty is common to business and probability can provide analytical tools to measure and control aspects of uncertainty.
Probabilities can be regarded as relative frequencies
The relative frequency is the probability that a particular event will take place.

Different Ways of Expressing Probability

There are many different ways probability can be expressed or written:
1) Descriptive word, certain, impossible
2) Ratio, "one in ten", "fifty fifty"
3) Percentage, 16%
4) Fraction, 1/2
5) Decimal, 0.5
All probabilities can be expressed in percentages.
There is another way of expressing a probability and that is as a decimal fraction.
The most common method used when working with statistics is as decimal fraction.

Subjective Probability

This type of probability is based on an estimate
It may be based on market research or experience but it will not involve any calculations.

Emphirical Probability

This is based on experimental data
As you continue to experiment the probability of a particular event will approach a limit.
This limit is called the Classical Probability

This can be calculated with the following formula:

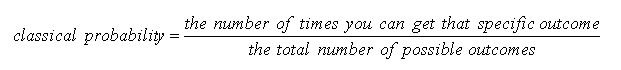The list of possible outcomes is known as the sample space.
The most interesting part about probability is calculating how often an event "will" occur to how often it "could" occur.

Theoretical Probability

Similar to emphirical approach except that you can work out the probability before actually conducting the experiment.

EQ: probability = (the number of ways a specific outcome can occur) / (the total number of possible outcomes)
This assumes all outcomes are equally as likely.

Common Terms

• Outcome (w) - the outcome of an experiment or trial

• Sample space / Probability space (?) - the set of possible outcomes of an experiment

The probability of an outcome P(w) can be defined as:

• Event - a set of outcomes or subset of the sample space.

If A is an event then

• Union - The set of outcomes in one event or in another event.

If A and B are events, then the union is A U B

• Intersection - The set of outcomes in two events.

If A and B are events, then the intersection is A N B or AB

• Complement - The set of outcomes not in an event

If A is an event, then the complement is Ac

• Empty Set - This contains no outcomes

• Mutually Exclusive - The occurrences in one event are not present in another event.

What is Probability Theory ?

Most introductions to probability theory treat discrete probability distributions and continuous probability distributions separately
This is the foundation of every aspect of Quantitative finance.
The use of the term stochastic to mean based on the theory of probability