Standard Deviation
This is the square root of the variance
The standard deviation can only be used with Interval Data and Ratio Data
This summarises an average distance of all the scores from the mean and uses the sum of squares
This measure is much more suitable for large data sets
The units of standard deviation are the same as the units of the original data.
What is wrong with using the Variance as a measure of disperson ?
The problem with using the variance is that it does not have the same units as the observations themselves.
Lets go back to our example at the top of the page.
In this example the variance gives us a percentage squared which doesn't have an obvious interpretation.
But if we take the square root of the variance then this has the same units as the observations themselves.
The standard deviation is the square root of the Veriance.
What is the Standard Deviation ?
The standard deviation is a measure of dispersion.
The standard deviation is the square root of the Veriance.
The standard deviation is the square root of the average of the squared deviations from the mean.
Finding the standard deviation of a dispersion gives a much better indication than just finding the mean since it uses all the values in the calculation.
The standard deviation shows the dispersion of values around the arithmetic mean.
Standard Deviations are usually referred to as above or below the mean, rather than plus or minus
What does the Standard Deviation tell us ?
The standard deviation shows the dispersion of values around the arithmetic mean.
The smaller the standard deviation the smaller the dispersion
The larger the standard deviation the more spread out the observations
Estimating the Standard Deviation (by dividing the range by 4)
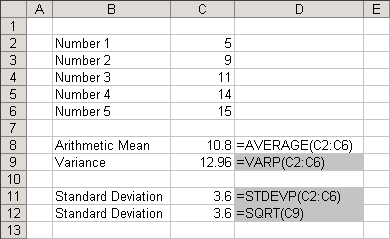
If you have a sample you can use one of the Excel functions (see below).
However of you have rough estimates (without any actual data) then you estimate the standard deviation.
First step is to calculate the "Range" - this is the largest values minus the smallest value
Lets assume that 95% of the values will fall within this Range .
We know that 2 standard deviations in a normal distribution contains about 95% of values.
This tells us that 95% of the values will be covered by 4 standard deviations (remember 2 positive and 2 negative)
Therefore if we divide the range by 4 we have an estimate of the standard deviation.
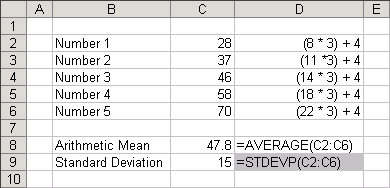
Calculating the Standard Deviation on a Sample
The standard deviation is just the positive square root of the variance.
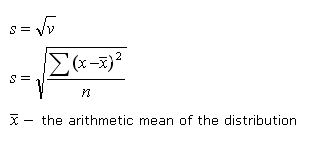 |
 |
 |
For more examples of this function please refer to the following pages:
STDEV.S - (2010 - STDEV) The standard deviation based on a sample.
STDEVA - The standard deviation based on a sample (including text and logical values).
Sample - N-1 - pg28
Population - N pg 28
Calculating the Standard Deviation on a Population
For more examples of this function please refer to the following pages:
STDEV.P - (2010 - STDEVP) The standard deviation based on an entire population.
STDEVPA - The standard deviation based on an entire population (including text and logical values).
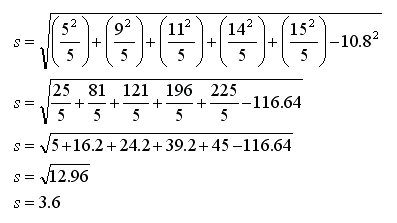
Alternative Formula
This alternative equation is often referred to as the mean of the squares minus the square of the means.
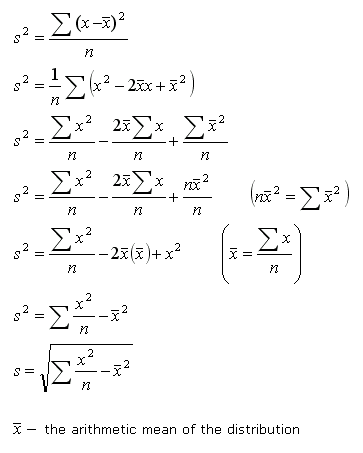 |
 |
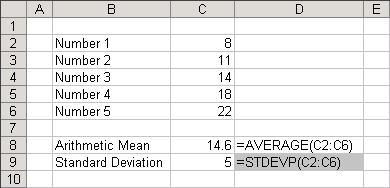
Shifting Standard Deviation
Original Values
Lets find the mean and the standard deviation for the following set of values:
 |
Adding a constant "c"
Lets find the mean and the standard deviation for the same set of values which have been increased by a constant amount.
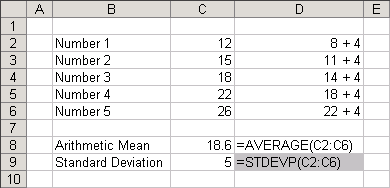 |
If each number is increased by a constant value "c" what happens to the mean and the standard deviation ?
If we have the following relationship:
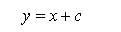 |
The mean value is also increased by the constant value.
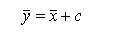 |
The standard deviation remains the same.
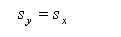 |
Multiplying by a constant "c"
Lets find the mean and the standard deviation for the same set of values which have been multiplied by a constant amount.
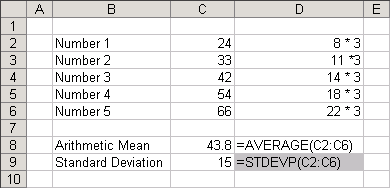 |
If each number is multiplied by a constant value "c" what happens to the mean and the standard deviation ?
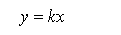 |
The mean value is also multiplied by the constant value.
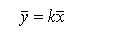 |
The standard deviation is multiplied by the absolute value of the constant.
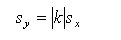 |
Adding and Multiplying
Lets find the mean and the standard deviation for the same set of values which have been multiplied by a constant amount and then
 |
The mean value is multiplied by the constant and then increased
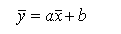 |
The standard deviation is multiplied by the absolute value of the constant.
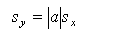 |
© 2025 Better Solutions Limited. All Rights Reserved. © 2025 Better Solutions Limited TopPrevNext