Matrix Functions
| MDETERM | The matrix determinant of an array. |
| MINVERSE | The inverse matrix of an array. |
| MMULT | The matrix product of two arrays. |
| MUNIT | (2013) The unit matrix or the specified dimension. |
| TRANSPOSE | The matrix transposed (i.e. with its orientation changed). |
| MDETERM The matrix determinant of an array. |
| MINVERSE The inverse matrix of an array. |
| MMULT The matrix product of two arrays. |
| MUNIT (2013) The unit matrix or the specified dimension. |
| TRANSPOSE The matrix transposed (i.e. with its orientation changed). |
Vectors and Matrices
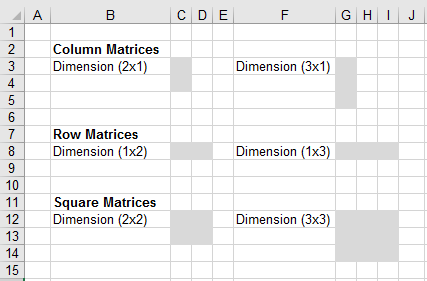
Rectangular arrays of numbers are called matrices.
A matrix can be represented as any small table of numbers.
A single column matrix is called a column vector.
A single row matrix is called a row vector.
The dimension of a matrix is written as (rows x columns)
A matrix is said to be square if it has the same number of rows and columns.
 |
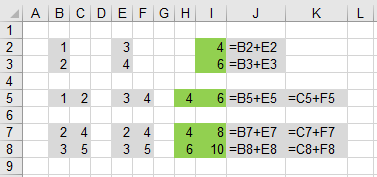
Adding Matrices
You can only add matrices that have the same dimension.
The result is the sum of the corresponding entries
There is no special Excel function to add because you can use straight addition.
 |
Identity Matrix
An identity matrix is a square matrix which contains all zeros except the main diagonal contains ones
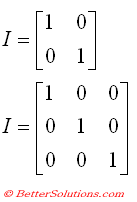 |
The inverse of a matrix is the matrix which when multiplied together gives the identity matrix.
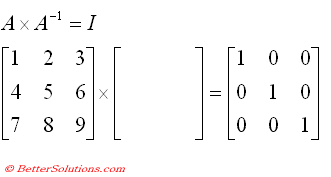 |
Include a SS
[] * [MINVERSE] = [identity]
MINVERSE
The MINVERSE function returns the inverse of the matrix as an array formula.
This is usually entered as an array function and therefore must be entered with (Ctrl + Shift + Enter).
To find out more about Array Formulas and Functions, please refer to the Array Formulas section.
Only square matrices "can have" inverses. Not all square matrices have inverses.
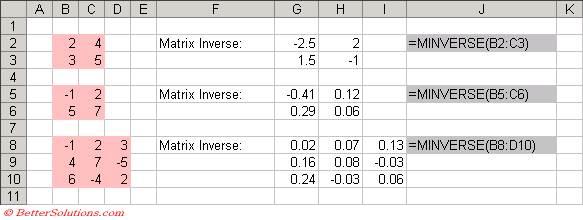 |
To prove that these are in fact the correct inverses we need to multiply the two matrices together. This is shown below.
A matrix that has no inverse has a determinant of zero and is said to be singular.
Not all square matrices have inverses.
A square matrix with an inverse is called "invertible" or "nonsingular".
A square matrix with no inverse is called "noninvertible" or "singular".
MMULT
The MMULT function returns the product of two matrices.
You must have a common dimension in the matrices that you want to multiple together.
The number of columns for one must equal the number of rows for the other.
This is usually entered as an array function and therefore must be entered with (Ctrl + Shift + Enter).
Matrix A multiplied by Matrix B is not the same as Matrix B multiplied by Matrix A (i.e. matrix multiplication is not commutative).
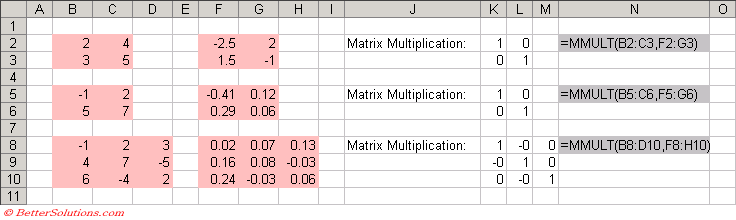 |
It is possible to use matrices to solve linear equations.
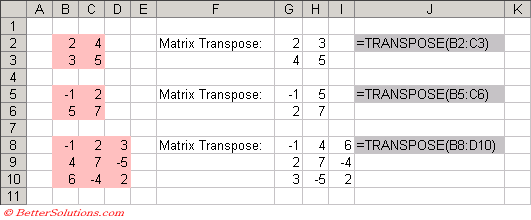
TRANSPOSE
The TRANSPOSE function will transpose a matrix and return an array formula.
Transposing an array converts rows into columns and columns into rows.
The transpose of a column vector will be a row vector.
This is usually entered as an array function and therefore must be entered with (Ctrl + Shift + Enter).
The first row of the input array becomes the first column of the output array.
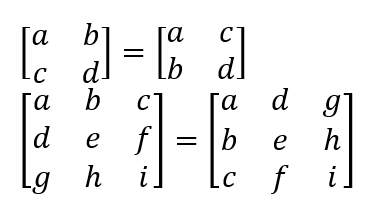 |
 |
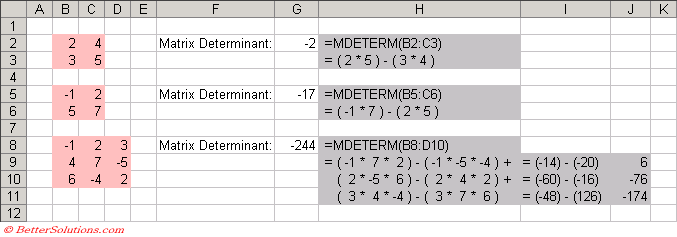
MDETERM
The MDETERM function returns the matrix determinant as an array formula.
This function only has an accuracy of 16 digits so a singular array may return a result that differs by 1E-16.
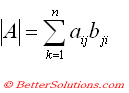 |
 |
MUNIT
The MUNIT function return the unit matrix or the specified dimension.
This function was added in Excel 2013.
Solving Simultaneous Linear Equations
You can use the inverse of a matrix to solve a set of equations.
This can be converted into matrix notation
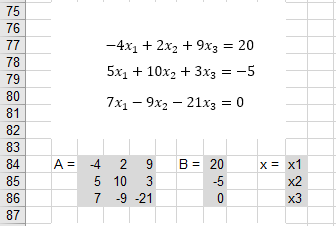 |
The solution can be found by multiplying both sides by the inverse of A
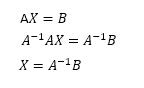 |
There is not always a solution.
Ax = b has a unique solution only if the matrix A is squares and has an inverse.
Important
When using the MDETERM, MINVERSE and MMULT functions every cell in the array must contain a numeric value. If not the function will return #VALUE!
A matrix with "m" rows and "n" columns is said to be of order (m * n). When "m" and "n" are equal then the matrix is said to be square.
Two matrices are said to be identical if every element in one matrix equals the corresponding element in the other matrix.
Matrix multiplication is not commutative so (A * B) does not equal (B * A).
Matrix division is undefined.
An identity matrix is a square matrix that contains all zeros except the main diagonal contains the value 1.
© 2026 Better Solutions Limited. All Rights Reserved. © 2026 Better Solutions Limited TopPrevNext